Características
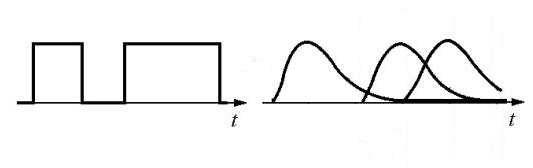
Em telecomunicações, a interferência entre símbolos (ISI – Intersymbol Interference) é uma forma de distorção do sinal na qual um símbolo interfere nos símbolos subsequentes. Esse fenômeno possui um efeito similar ao ruído, assim fazendo a comunicação menos confiável. As causas da ISI podem ser tanto a propagação de sinais por múltiplos caminhos no ar quanto pelo fato de os canais de transmissão possuírem uma largura de banda limitada. A primeira se dá pelo fato que um sinal, ao ser transmitido pelo ar pode assumir vários caminhos até chegar ao receptor, devido às várias reflexões a que ele é submetido pelo caminho, bem como por possíveis refrações. Sabendo que esses vários caminhos possuem comprimentos diferentes, podemos concluir que cada sinal chegará ao receptor em momentos diferentes, fazendo com que cada símbolo recebido apresente parte dele dentro do “slot” reservado ao símbolo adjacente. A segunda causa ocorre pelo fato de que cada canal de transmissão funciona como um filtro, que atenua frequências a partir de certa frequência de corte. Dessa forma, essa filtragem imprópria do pulso provoca um espalhamento do mesmo no tempo, o que faz com que ele interfira no símbolo seguinte, causando a ISI. Esse caso pode ser exemplificado na figura a seguir.
Consequências para a comunicação
A implicação mais evidente e importante da ISI nas telecomunicações diz respeito ao aumento da probabilidade de erro de bit na recepção. Analisando como a ISI afeta o sinal podemos perceber que o pulso espalhado pode afetar o pulso seguinte de tal forma que sua amplitude no ponto de amostragem seja alterada a tal ponto que um símbolo referente ao bit 0 que tenha sido transmitido seja identificado como bit 1 na recepção, e vice-versa. Dessa forma a confiabilidade do sistema é comprometida, de forma que maneiras de se combater a ISI tenham que ser implementadas. Alguns dos processos adotados para tal fim serão abordados a seguir.
Soluções desenvolvidas ou em andamento
A eliminação do efeito de interferência intersimbólica consiste em modelar adequadamente as funções de transferência dos filtros do transmissor e do receptor, de forma a otimizar a recepção através da minimização do efeito. Existem dois métodos clássicos de modelagem destes filtros de forma a diminuir a ISI, sendo que um é teórico (irrealizável fisicamente), enquanto que o outro é amplamente utilizado na prática.
Primeiro Método de Nyquist (ISI zero)
O primeiro método de nyquist consiste em usar uma função de transferência equivalente he(f), tal que a resposta ao impulso unitário satisfaça a seguinte equação:
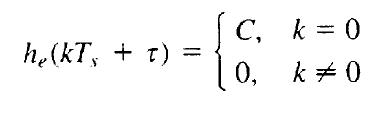
Onde k é um inteiro, Ts é o período de clock de símbolo (amostra), τ é o deslocamento nos períodos de clock no receptor quando comparado com os períodos de clock dos símbols de entrada, e C é uma constante diferente de zero. Isto é, para um pulso de entrada quadrado de nível a no filtro do transmissor em t = 0, o pulso recebido será a.he(t). Este pulso seria a.C em t = τ, mas não causaria interferência nos outros períodos de amostragem porque he(kTs+τ) = 0 para k diferente de zero.
Supondo que se escolhesse uma função sinc(x) para he(t); em particular, tendo τ = 0 e he(t) será:

Onde fs = 1/Ts. Essa resposta ao impulso satisfaz o primeiro critério de Nyquist para zero ISI, conforme mostrado na primeira equação. Consequentemente, se os filtros de transmissão e recepção forem projetados de tal forma que a função de transferência equivalente do enlace seja:

Não haverá ISI. A largura de faixa absoluta desta função de transferência será fs/2; assim, além de evitar a ISI, este método garante que a mínima banda possível será consumida.
No entanto, o primeiro método de Nyquist tem duas dificuldades práticas muito grandes:
- a) A função de transferência resultante deve ser, na frequência, um retângulo entre –B e B, correspondente a um filtro passa-baixa ideal, o que é fisicamente irrealizável.
- b) A sincronização de clock no circuito decodificador de amostras deve ser perfeita, o que é muito difícil e sujeito a falhas.
Devido a essas dificuldades, outras formas de função de transferência com uma largura de faixa maior devem ser consideradas. A ideia é encontrar uma resposta que passe por zero em pontos de amostragem adjacentes.
Técnica do Cosseno levantado
O filtro do tipo cosseno levantado tem a função de transferência:

Onde B é a largura de faixa absoluta e os parâmetros fl e fΔ são:
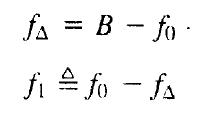
fo é a frequência em que ocorre queda de 6 dB no filtro do tipo cosseno levantado. O fato de rolloff é definido como sendo:

A característica deste filtro é mostrado na figura adiante. A resposta ao impulso correspondente é:
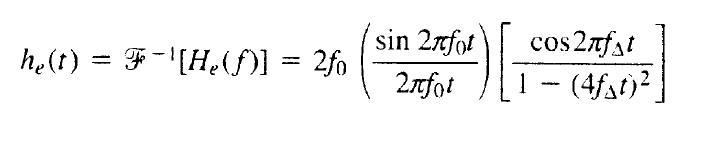
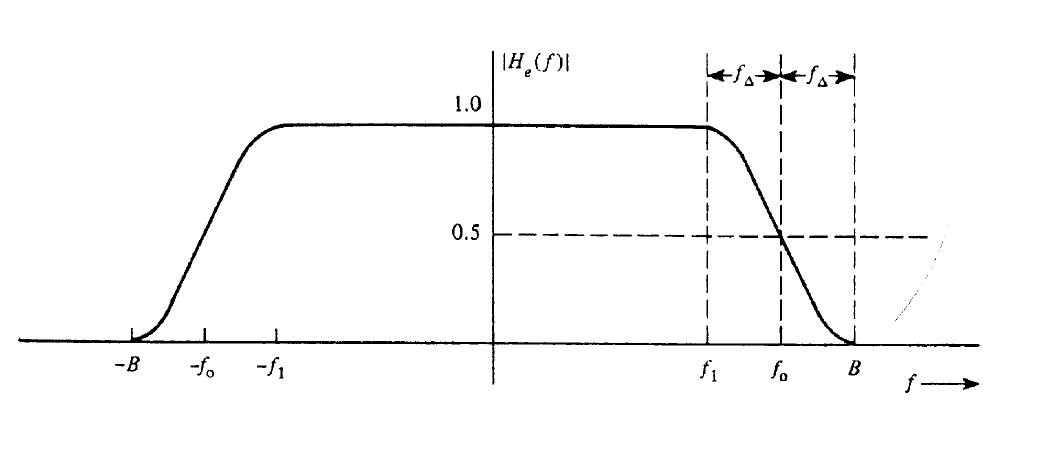

Gráficos da resposta em frequência e da resposta ao impulso unitário são mostrados nas duas figuras acima, para fatores de rolloff r = 0, r = 0.5 e r = 1. A característica da resposta para fator nulo é o caso descrito no primeiro método de Nyquist: menor banda possível, com fo = B e com a reposta ao impulso no formato sinc. As figuras mostram também que, na medida em que o fator de rolloff aumenta, fica mais fácil a implementação, pois a filtragem torna-se realizável e a sincronização mais fácil.
A taxa de símbolos que o sistema pode suportar sem que ocorra ISI relaciona-se com a largura de faixa absoluta do sistema e com o fator de rolloff característico da filtragem por cosseno levantado. A última figura mostra que a resposta ao impulso passa por zeros a cada t = n/2fo, para n diferente de zero. Assim, o cosseno levantado satisfaz ao primeiro critério de Nyquist se for usado τ = 0 e o tempo de amostragem como sendo Ts = 1/2fo. A taxa correspondente de símbolos será D = 1/Ts = 2fo símbolos/seg. A taxa de símbolos suportada pelo sistema será:
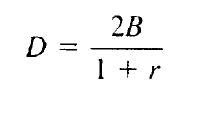
Onde B é a largura de faixa absoluta do sistema e r é o fator de rollof.
Experimentos
Referências
[1] COUCH II, L. W. Digital and Analog Communication Systems. 5ª ed. Prentice Hall International Editions, Novembro 1996.
[2] LATHI, B. P. Modern Digital and Analog Communication Systems. 3ª ed. Oxford University Press, 1998.